Week 4: Scientific Computing in Python¶
This week, you will learn how to do scientific computing in Python. As we learned from first lecture, Numpy is a fundamental package for scientific computing.
The goal of this assignment is to gain comfort creating, visualizating, and computing with numpy array. By the end of the assignment, you should feel comfortable:
- Creating new Numpy arrays using
linspaceandarange - Computing basic formulas with Numpy arrays
- Performing reductions (e.g.
mean,stdon numpy arrays) - Making 1D line plots
Grading:
- Total: 100
- Complete the example code: 20
- Exercise: 26
- Assignment: 44
- Comments clearly and concisely explain the purpose and reasoning behind code: 10
1. Importing and Examining a New Package¶
This will be our first experience with importing a package which is not part of the Python standard library.
import numpy as np
# find out what version we have
np.__version__
'2.0.2'
The numpy documentation is crucial!
2. NDArrays¶
The core class is the numpy ndarray (n-dimensional array). The n-dimensional array object in NumPy is referred to as an ndarray, a multidimensional container of homogeneous items – i.e. all values in the array are the same type and size. These arrays can be one-dimensional (one row or column vector), two-dimensional (m rows x n columns), or three-dimensional (arrays within arrays).
The main difference between a numpy array an a more general data container such as list are the following:
- Numpy arrays can have multiple dimensions (while lists, tuples, etc. only have 1)
- Numpy arrays hold values of the same datatype (e.g.
int,float), whilelistscan contain anything. - Numpy optimizes numerical operations on arrays. Numpy is fast!
from IPython.display import Image
Image(url='http://docs.scipy.org/doc/numpy/_images/threefundamental.png')
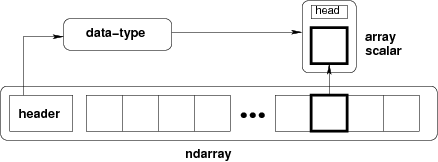
2.1 Create array from a list¶
# create an array from a list
a = np.array([9,0,2,1,0])
# find out the datatype
a.dtype
dtype('int64')
# find out the shape
a.shape
(5,)
# what is the shape
type(a.shape)
tuple
# another array with a different datatype and shape
b = np.array([[5,3,1,9],[9,2,3,0]], dtype=np.float64)
# array with 3 rows x 4 columns
a_2d = np.array([[3,2,0,1],[9,1,8,7],[4,0,1,6]])
a_2d
array([[3, 2, 0, 1],
[9, 1, 8, 7],
[4, 0, 1, 6]])
# check dtype and shape
b.dtype
(dtype('float64'), (2, 4))
# check data shape
b.shape
(2, 4)
Important Concept: The fastest varying dimension is the last dimension! The outer level of the hierarchy is the first dimension. (This is called "c-style" indexing)
2.2 Create arrays using functions¶
# create some uniform arrays
c = np.zeros((9,9))
d = np.ones((3,6,3), dtype=np.complex128)
e = np.full((3,3), np.pi)
e = np.ones_like(c)
f = np.zeros_like(d)
# Random arrays
g = np.random.rand(3,4)
The np.arange() function is used to generate an array with evenly spaced values within a given interval. np.arange() can be used with one, two, or three parameters to specify the start, stop, and step values. If only one value is passed to the function, it will be interpreted as the stop value:
# create some ranges
np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# arange is left inclusive, right exclusive
np.arange(2,4,0.25)
array([2. , 2.25, 2.5 , 2.75, 3. , 3.25, 3.5 , 3.75])
Similarly, the np.linspace() function is used to construct an array with evenly spaced numbers over a given interval. However, instead of the step parameter, np.linspace() takes a num parameter to specify the number of samples within the given interval:
# linearly spaced
np.linspace(2,4,20)
array([2. , 2.10526316, 2.21052632, 2.31578947, 2.42105263,
2.52631579, 2.63157895, 2.73684211, 2.84210526, 2.94736842,
3.05263158, 3.15789474, 3.26315789, 3.36842105, 3.47368421,
3.57894737, 3.68421053, 3.78947368, 3.89473684, 4. ])
Note that unlike np.arange(), np.linspace() includes the stop value by default (this can be changed by passing endpoint=True). Finally, it should be noted that while we could have used np.arange() to generate the same array in the above example, it is recommended to use np.linspace() when a non-integer step (e.g. 0.25) is desired.
np.linspace(2,4,20, endpoint = False)
array([2. , 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2,
3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9])
Exercise 1: Create a 1D array ranging from 0 to 100 (including 100) with an interval of 5. (5 points)¶
2.3 Create two-dimensional grids¶
x = np.linspace(-4, 4, 9)
x
array([-4., -3., -2., -1., 0., 1., 2., 3., 4.])
y = np.linspace(-5, 5, 11)
y
array([-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.])
#If you want every combination of (x, y) pairs, meshgrid helps you build two 2D arrays that represent these combinations.
x_2d, y_2d = np.meshgrid(x, y)
# x_2d repeats the x array across rows.
x_2d
array([[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.]])
# y_2d repeats the y array across columns.
y_2d
array([[-5., -5., -5., -5., -5., -5., -5., -5., -5.],
[-4., -4., -4., -4., -4., -4., -4., -4., -4.],
[-3., -3., -3., -3., -3., -3., -3., -3., -3.],
[-2., -2., -2., -2., -2., -2., -2., -2., -2.],
[-1., -1., -1., -1., -1., -1., -1., -1., -1.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[ 2., 2., 2., 2., 2., 2., 2., 2., 2.],
[ 3., 3., 3., 3., 3., 3., 3., 3., 3.],
[ 4., 4., 4., 4., 4., 4., 4., 4., 4.],
[ 5., 5., 5., 5., 5., 5., 5., 5., 5.]])
# You can now evaluate a function on this grid easily:
z_2d = x_2d + y_2d
z_2d
array([[-9., -8., -7., -6., -5., -4., -3., -2., -1.],
[-8., -7., -6., -5., -4., -3., -2., -1., 0.],
[-7., -6., -5., -4., -3., -2., -1., 0., 1.],
[-6., -5., -4., -3., -2., -1., 0., 1., 2.],
[-5., -4., -3., -2., -1., 0., 1., 2., 3.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-3., -2., -1., 0., 1., 2., 3., 4., 5.],
[-2., -1., 0., 1., 2., 3., 4., 5., 6.],
[-1., 0., 1., 2., 3., 4., 5., 6., 7.],
[ 0., 1., 2., 3., 4., 5., 6., 7., 8.],
[ 1., 2., 3., 4., 5., 6., 7., 8., 9.]])
Exercise 2 (10 points):¶
You are given two one-dimensional arrays:
xcontains 5 values evenly spaced between –2 and 2.ycontains 3 values evenly spaced between –1 and 1.
Write a Python program that does the following:
- Use
numpy.meshgridto create two 2D arraysXandYfromxandy. - Compute a new 2D array
Zdefined as ( Z = X^2 + Y^2 ). - Print the shapes of
X,Y, andZ. - In a code comment, briefly explain what the values in
Zrepresent in terms ofXandY.
3. Indexing in Numpy¶
Indexing in NumPy allows you to access and modify elements, rows, columns, or subarrays of an array. Basic indexing is similar to lists.
# get some individual elements of xx
x_2d[0,0], x_2d[-1,-1], x_2d[3,-5]
(np.float64(-4.0), np.float64(4.0), np.float64(0.0))
# get some whole rows and columns
x_2d[0].shape, x_2d[:,-1].shape
((9,), (11,))
# get some ranges
x_2d[3:10,3:5].shape
(7, 2)
There are many advanced ways to index arrays. You can read about them in the manual. Here is one example.
# use a boolean array as an index
idx = x_2d<0
x_2d[idx].shape
(44,)
Exercise 3: Get the last two columns of y_2d array. (5 points)¶
# two dimensional grids
x = np.linspace(-2*np.pi, 2*np.pi, 100)
y = np.linspace(-np.pi, np.pi, 50)
xx, yy = np.meshgrid(x, y)
xx.shape, yy.shape
((50, 100), (50, 100))
f = np.sin(xx) * np.cos(0.5*yy)
Visualizing Arrays with Matplotlib¶
It can be hard to work with big arrays without actually seeing anything with our eyes! We will now bring in Matplotib to start visualizating these arrays. For now we will just skim the surface of Matplotlib. Much more depth will be provided in future lectures.
from matplotlib import pyplot as plt
plt.pcolormesh(f)
<matplotlib.collections.QuadMesh at 0x10eb71bb0>
4.2 Manipulating array dimensions¶
# transpose
plt.pcolormesh(f.T)
<matplotlib.collections.QuadMesh at 0x10ec778b0>
f.shape
(50, 100)
np.tile(f,(6,1)).shape
(300, 100)
# tile an array
plt.pcolormesh(np.tile(f,(6,1)))
<matplotlib.collections.QuadMesh at 0x10ecdaf70>
4.3 Broadcasting¶
Broadcasting is an efficient way to multiply arrays of different sizes
from IPython.display import Image
Image(url='http://scipy-lectures.github.io/_images/numpy_broadcasting.png',
width=720)
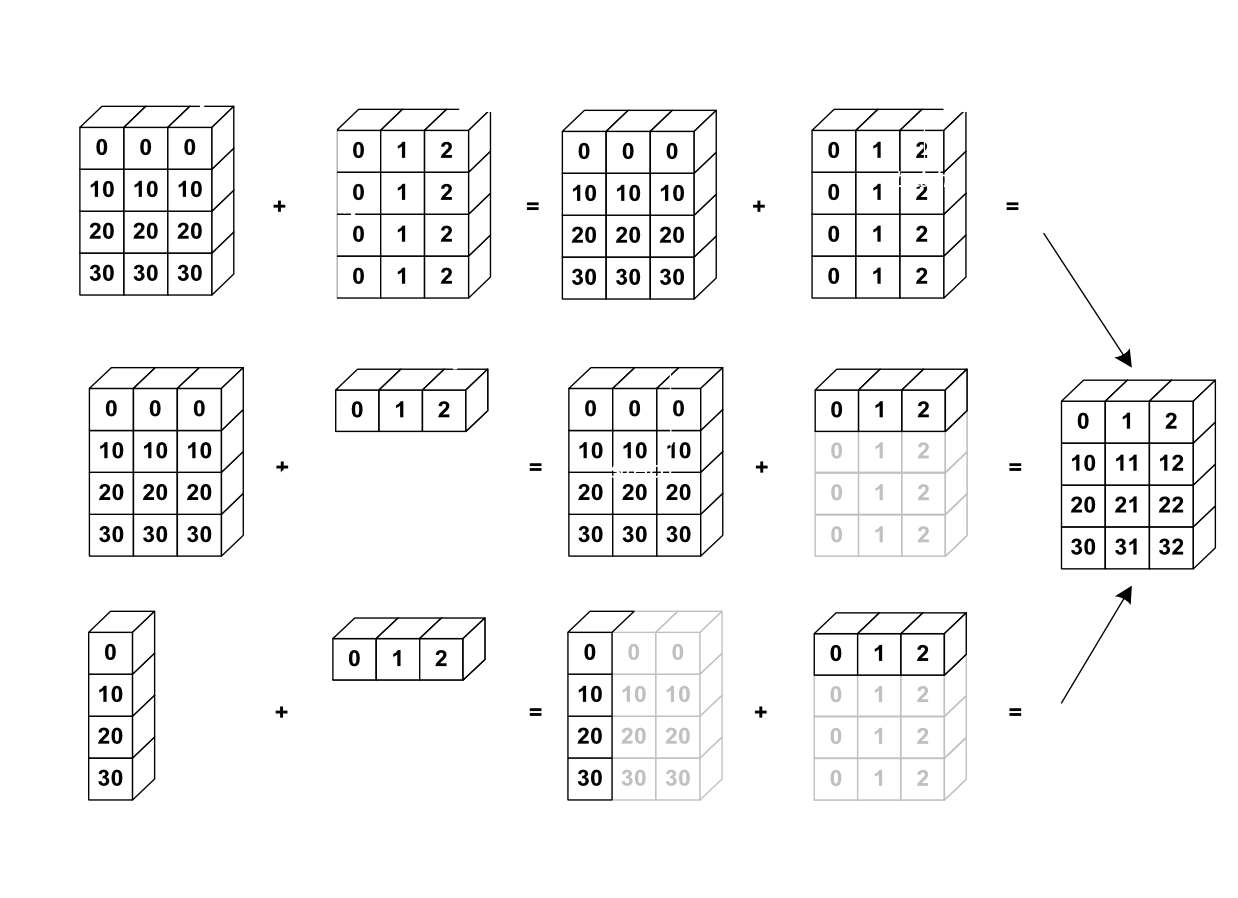
# multiply f by x
print(f.shape, x.shape)
g = f * x
print(g.shape)
(50, 100) (100,) (50, 100)
# multiply f by y
print(f.shape, y.shape)
h = f * y
print(h.shape)
(50, 100) (50,)
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) Cell In[48], line 3 1 # multiply f by y 2 print(f.shape, y.shape) ----> 3 h = f * y 4 print(h.shape) ValueError: operands could not be broadcast together with shapes (50,100) (50,)
# use newaxis special syntax
y_new = y[:,np.newaxis]
h = f * y_new
print(h.shape)
(50, 100)
Exercise 4: What is the difference between y and y_new? Why f * y gives an error, but f * y_new doesn't? (3 points)¶
4.4 Reduction Operations¶
# sum
g.sum()
np.float64(-3083.038387807155)
# mean
g.mean()
np.float64(-0.616607677561431)
# std
g.std()
np.float64(1.6402280119141424)
# apply on just one axis
# Mean of each row (calculated across columns)
g_xmean = g.mean(axis=1)
# Mean of each column (calculated across rows)
g_ymean = g.mean(axis=0)
plt.plot(x, g_ymean)
[<matplotlib.lines.Line2D at 0x10ee70a00>]
plt.plot(g_xmean, y)
[<matplotlib.lines.Line2D at 0x10eedabe0>]
5. Missing data¶
Most real-world datasets – environmental or otherwise – have data gaps. Data can be missing for any number of reasons, including observations not being recorded or data corruption. While a cell corresponding to a data gap may just be left blank in a spreadsheet, when imported into Python, there must be some way to handle "blank" or missing values.
Missing data should not be replaced with zeros, as 0 can be a valid value for many datasets, (e.g. temperature, precipitation, etc.). Instead, the convention is to fill all missing data with the constant NaN. NaN stands for "Not a Number" and is implemented in NumPy as np.nan.
NaNs are handled differently by different packages. In NumPy, all computations involving NaN values will return nan:
data = np.array([[2.,np.nan,1.89],
[1.1, 0.0, np.nan],
[3.2, 0.74, 2.1]])
#Count missing values
missing_count = np.isnan(data).sum()
print(missing_count)
2
# Mean np.mean returns nan if there’s any nan in the data, because the missing value contaminates the calculation.
np.mean(data)
np.float64(nan)
# Use nanmean function to ignore missing values:
np.nanmean(data)
np.float64(1.71625)
# Remove missing values:
clean_data = data[~np.isnan(data)]
clean_data
array([2. , 1.89, 1.1 , 0. , 3.2 , 0.74, 2.1 ])
Exercise 5: Create a new array that replace missing values in data with mean. (3 points)¶
6. Assignment¶
6.1. Create two 2D arrays representing coordinates x, y. Both should cover the range (-2, 2) and have 100 points in each direction. (6 points)¶
Hint: use the meshgrid function
6.2. Visualize each 2D array using pcolormesh (6 points)¶
Use the correct coordiantes for the x and y axes.
6.3 From your cartesian coordinates, create polar coordinates $r$ and $\varphi$ (6 points):¶
$r = \sqrt{x^2 + y^2}$
$\varphi = atan2(y,x)$
You will need to use numpy's arctan2 function. Read its documentation.
6.4. Visualize $r$ and $\varphi$ on the 2D $x$ / $y$ plane using pcolormesh (6 points)¶
6.5 Caclulate the quanity $f = \cos^2(4r) + \sin^2(4\varphi)$ (5 points)¶
6.6 Plot f on the $x$ / $y$ plane (5 points)¶
6.6 Plot the mean of f with respect to the x axis, as a function of y (5 points)¶
6.7 Plot the mean of f with respect to the y axis, as a function of x (5 points)¶